Articolo di Valentina apparso su “il Bo” l’11 giugno 2014.
Siete vivi grazie ad un’operazione al cuore: oltre che al cardiochirurgo che vi ha operati è possibile che dobbiate essere riconoscenti ad un matematico e alla sua équipe. Il vostro specifico cuore è infatti stato “modellato matematicamente” al computer prima dell’operazione, di modo da essere in grado di simulare le conseguenze dell’intervento e poter prevedere gli scenari conformi a tecniche diverse. Come anticipare il futuro, sapendo di poter tornare indietro e correggere il tiro.
Fantascienza? Nient’affatto: matematica applicata. Se ne occupa da anni Alfio Quarteroni, docente ai politecnici di Milano e di Losanna, che utilizza per il sistema cardiocircolatorio una metodologia ormai di routine nell’ingegneria civile, ma che può essere estesa ad altri ambiti, diventando, nel caso del cuore, una tecnica all’avanguardia, come ha raccontato recentemente in una lezione all’Università di Padova.
Si tratta di “tradurre” un problema reale e quindi complesso –composto da fenomeni di natura diversa e che agiscono su scale differenti– in un insieme di equazioni matematiche in grado di descriverlo, e di risolverle nel campo di interesse: il cuore, con la sua forma specifica, o, nel caso più di routine della progettazione ingegneristica, un edificio da progettare, un ponte, una frana, una diga, un terremoto. Quello che si vuole ottenere è un modello rappresentativo della realtà con il quale valutare il comportamento di alcune prefissate grandezze fisiche.
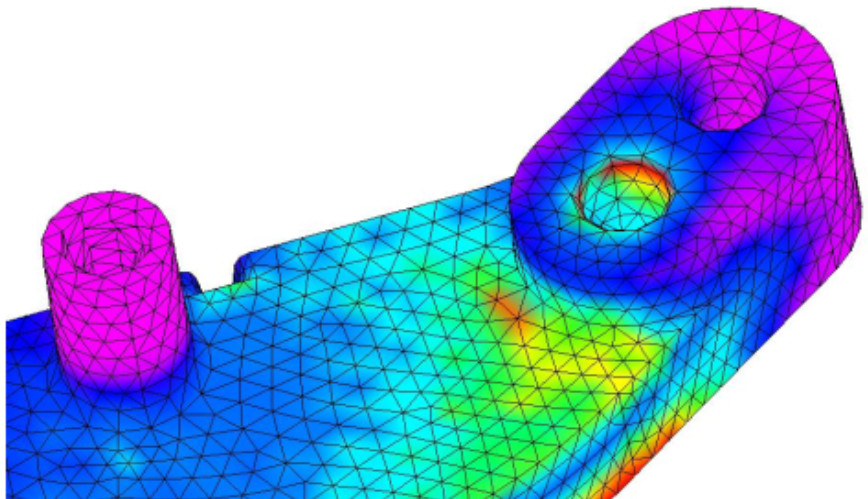
Le equazioni che descrivono i fenomeni fisici sono equazioni “alle derivate parziali”, in cui cioè sono coinvolte le variazioni infinitesime nello spazio e nel tempo delle grandezze che descrivono il problema: velocità, densità, temperatura ecc. Questo genere di equazioni raramente ha una soluzione analitica esplicita, ma esse devono essere risolte in via approssimata con metodi iterativi che offrano una soluzione quantitativa, sufficientemente vicina alla soluzione reale per il problema in esame. Le equazioni, oltretutto, descrivono il comportamento di variabili discrete, cioè di grandezze puntuali (la velocità di un punto, lo spostamento di una data coordinata) ma devono essere applicate a corpi continui, quali sono quelli reali. Questo viene ottenuto “discretizzando” il continuo in sottodomini più piccoli alle cui “estremità” (tecnicamente chiamate nodi) vengono risolte le equazioni. Più fitta è la maglia di suddivisioni, maggiore è l’aderenza alla realtà.
Poiché, in questo modo, aumentano vertiginosamente i set di equazioni da risolvere, e, per ciascuno di essi, la procedura iterativa richiede un elevato numero di singole operazioni da eseguire, si capisce bene come si renda necessario l’utilizzo del computer e di quella che viene chiamata dagli specialisti analisi numerica, ossia l’insieme di tecniche per risolvere problemi di questa natura. Il calcolatore ben si presta, infatti, a ripetere innumerevoli volte e in innumerevoli “posizioni” sequenze di operazioni sufficientemente semplici. La potenza di calcolo dei computer di cui oggi disponiamo, unita all’evoluzione delle tecniche risolutive, ha fatto sì che problemi che fino a qualche anno fa richiedevano settimane di “tempo macchina” per giungere ad una soluzione– “a convergenza” in gergo tecnico – oggi possano essere risolti nell’arco di mezza giornata di calcolo.
Quella che si ottiene non è, chiaramente, una rappresentazione reale nella sua totalità, ma un modello che è in grado di cogliere il fenomeno reale in modo sufficientemente fedele, ma che resta per sua natura intrinseca soggetto a semplificazioni. Non bisogna dimenticare infatti che si tratta di problemi di elevata complessità geometrica, in cui devono essere descritti comportamenti anche affatto diversi: lo scorrere del sangue in un vaso è un esempio tipico di problema “accoppiato”, in cui cioè la simulazione matematica deve riprodurre l’interazione macroscopica del fluido – il sangue– modellato con le equazioni “idrauliche” di Navier –Stokes, con la struttura – le pareti del vaso– soggetta alle leggi della meccanica dei solidi: il fronte di pressione del fluido trasferisce energia alle pareti del vaso che si dilatano, e poi queste, nella fase di compressione, la restituiscono al flusso. Ma c’è di più: nel caso di modelli biologici come la riproduzione del flusso sanguigno, è necessario simulare anche i comportamenti microscopici: l’influenza dello sforzo tagliante dovuto al flusso sull’orientamento, la deformazione e il danneggiamento delle cellule endoteliali e gli effetti dovuti al trasporto, alla diffusione e all’assorbimento delle componenti chimiche in gioco.
Fintanto che si modella una singola arteria, la potenza dei calcolatori odierni ci assiste, ma qualora si volesse schematizzare l’intero sistema circolatorio, un livello di dettaglio simile non sarebbe compatibile con i tempi di calcolo. Ecco quindi che Quarteroni e il suo team utilizzano una sorta di schema ad albero: l’aorta è riprodotta tridimensionalmente nella sua geometria reale e le equazioni sono impostate per tutte e tre le dimensioni dello spazio (oltre che nel tempo), le arterie invece sono dei percorsi monodimensionali (nella direzione del flusso), mentre i vasi terminali hanno dimensione nulla: in loro “esiste” solo il tempo, ma si trascurano i fenomeni spaziali.
Ragionare in questi termini, applicare cioè concetti teorici avanzati a problemi pratici, per raggiungere degli scopi prefissati con occhio ingegneristico, è la frontiera odierna della matematica, nei campi più disparati. Quarteroni, ad esempio, oltre a collaborare con numerosi ospedali per la modellazione del sistema cardiocircolatorio (Niguarda, Sacco, Policlinico a Milano; Borgo Trento a Verona, l’ospedale di Rovereto, il Centre Hospitalier Universitaire Vaudois a Losanna e altri), è stato il consulente di Alinghi per la Coppa America negli anni in cui l’imbarcazione, perfezionata grazie alle sue simulazioni, ha vinto la competizione. Inoltre ha modellato, insieme ai suoi collaboratoit, gli effetti fluidodinamici indotti dall’incrocio di trama e ordito nei costumi dei nuotatori olimpici delle migliori squadre, solo per citare le attività più importanti.
Valentina Berengo